What is an "unicursal maze"? In order to understand what an unicursal maze is, the concept of a maze needs to be defined.

A maze has several parts.

A maze has an entrance; This area is where a person would begin or start the maze.

A maze has an exit; This area is where, if the person reaches it, the maze is done and there's no more of the maze that the person must experience.

A maze has areas where a person must decide in what direction they need to travel. On roadways, these areas are often called "intersections" because two or more roads cross or "intersect" with one another.

Entrances, exits & intersections are the three basic parts for a typical maze.

This illustrated example is how a maze is thought of by many people. This small maze has an entrance, an exit & three intersections where a person needs to make a decision as to which direction to travel towards.

This maze also features an additional part: Areas where the player is forced to turn around or to backtrack from where they previously were. These areas are typically called "dead ends." In this illustrated example, there are three such "dead ends."

This type of maze, that has intersections and "dead ends," is typically called a "multicursal" maze. "Multi-" meaning 'many,' and "cursal" which is derived from the Latin word "cursus," which can mean "passage." "Multicursal maze" can then be thought of as a "Many passage" maze.

If a "multicursal" maze is a "many passages" maze, an "unicursal" maze can be translated by it's word parts as well. "Uni-" means "one" and "cursal" has been defined previously as "passage"; An "one passage" maze or a maze with no intersections and no "dead ends."

Here is an illustration of what an unicursal maze looks like:

In the study of unicursal mazes, the basic parts of a maze have been given terms:

• The entrance is the "start" of the maze, so it's called the "starting point."
• The exit is the "end" of the maze, so it's called the "end point."
• The intersections are areas where a decision must be made, so these are called "decision points."

The word "point" keeps being used. Why is that?

A maze can be thought of as a series of points. If you look at the unicursal maze before, it can be seen that it is comprised of points that are assembled in a series of evenly-spaced rows and columns. This illustration should make that concept clearer:

The rows and columns of points are called a "field." In this example, there are 4 columns and there are 4 rows. In the study of unicursal mazes, the word "maze" itself is not used (as will be made clearer later) and is replaced by the word "field." This maze would be considered a 4x4 (4 columns and 4 rows) "field."

A lot of mazes are constructed with the walls being a dark color and the passage (or "path") being a light color. This method of color choice is used so that a person can "figure out" a maze by drawing a line through the passage from the entrance to the exit. There's nothing wrong with this method of illustration; It's supposed to facilitate solving the maze and it does.

Yet in the study of unicursal mazes, this method of illustrating a maze by making the walls dark and leaving the passages empty doesn't facilitate the study of the maze itself. Such a type of illustration hinders the study of these mazes by emphasizing the walls and not the passages (the "path"). Instead, in the study of unicursal mazes, it is the path that is dark and the walls are not drawn as they are not necessary.

Here is that same unicursal maze using this new illustration method.

When this illustration method is used, two aspects of the maze stands out: The entrance and the exit.

In the prior illustration method (dark walls and empty passages), there had to be an "entrance" & an "exit" cutting through the outer wall. Such a feature is not necessary when studying an unicursal maze. In studying an unicursal maze, there are no "walls," just a "starting point" & an "end point." It doesn't matter from which direction the starting or ending point is approached or left, just that they are identified.

The starting point is identified as having a square as it's symbol.

The end point is identified by having a cross (a "plus") as it's symbol.

Why a square for the starting point & a cross for an ending point? There's no specific answer. I needed two symbols that were easy to draw, distinctive to draw with a limited amount of pixels & distinctive from one another.

You may think that there are no "decision points" in an unicursal maze but you'd be wrong. In an unicursal maze, the decision points are formed during the formation of the maze itself, not when a person is trying to "solve" a maze. To illustrate a decision point, a forward slash ("/") is used, as illustrated below:

Why a forward slash? Again, I needed a symbol that was easy to draw, distinct from all of the other symbols and also distinct with the limited amount of pixels available.

At this stage, calling this drawing a "maze" really isn't accurate. It's a "path" and that's the terminology that is formally used when discussing such creations. Why isn't this website called "Unicursal Path Research"? It has to do with the fact that the word 'path' can mean many things when the context isn't clear. It's easier to use the word "maze" (and, more specifically, the phrase "unicursal maze") to provide the necessary clarity.

In the illustration above, the path continues down after the decision point. However, the path could have gone to the right and still completed the maze at the same end point, as illustrated below:

Sometimes, the starting point can also be a "decision point." It's like in English grammar when, sometimes, the letter "y" is sometimes a vowel and not a consonent. In the case of this particular starting and end point, the starting point can be a decision point, as illustrated below:

Finally, all of these prior examples may seem attractive to the eye. However, when analyzing unicursal mazes, you want all of the points (even the non-decision point ones) to be visible for cataloging purposes. It just makes it easier to determine the exact anatomy of an unicursal path. However, having such a short distance between points causes the maze to look cluttered and confusing. In order to make the maze clearer to analyze, the distance between points is increased to make the corners more distinct. Here's a "real world" example of a completed unicursal path:

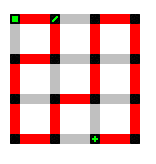
In conclusion, an unicursal maze is a path that never branches from the starting point to the ending point. Along the path, there are decision points where the path could have gone in another direction and still concluded at the end point.

The above primer is, by no means, the totality of knowledge when it comes to unicursal mazes but it should give people unfamiliar with this research a base amount of knowledge about the field of study.