In relation to Unicursal Maze Research, a path starts with a 'start point' and ends with an 'end point.' As a refresher, a start point has a solid green square and an end point has a green cross on it.

Here is a typical path that has a start point and an end point.

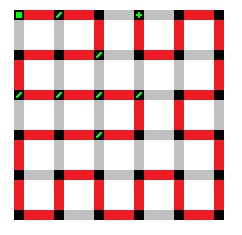
When a start point and an end point are on a field, they are referred to as a 'pair' (as in 'a pair of start and end points'). Look at the maze above to see such a pair as part of an actual unicursal maze.

In the pursuit of Unicursal Maze Research, though, a 'pair' may be classified as either an 'original pair' or a 'derivative pair.'

In order to explain the difference between an original pair and a derivative pair, it is helpful to understand the challenges of creating unicursal mazes as opposed to a conventional multicursal (or "normal) maze.

In a multicursal maze, the start and end point may be any of the two points in a field. The reason for this infinite amount of flexibility is because multicursal mazes have 'dead ends,' or places in the maze where the path stops. Multicursal mazes also have 'intersections,' or places in the maze where the path deviates into two or more directions. With 'intersections' and 'dead ends,' the most efficient path from the start point to the end point is always less than the total number of available points in the field. Here is an example of one such multicursal maze:

In an unicursal maze, there are many more limitations imposed upon where a start and end point may be placed. An unicursal maze must begin at the start point, end at an end point and pass through every single other point first only once before reaching that end point. By having to pass through every single point first and only once before reaching the end point, unicursal mazes do not have either 'intersections' or 'dead ends.' Here is an example of a simple unicursal path:

Unicursal mazes can not simply end anywhere on a field as a result of not having intersections and dead ends; They may only end at certain points on a field. As an activity, here is a 4x4 field with a start point already assigned to the upper-leftmost point. Using this template, draw unicursal mazes that end at as many points on the field as you can. Obviously, the start point is ineligible (it has already been 'entered' being the first point in the path).

After a while, a pattern will emerge as to where an unicursal path may end given to where the starting point is. The answer is given below:

As it may be seen, not every point in a field may be an end point. Looking at this field, every other point in the field may be an eligible end point. Or, in other words, every even-numbered point on the field may be an eligible end point. If the start point is counted as "one," and every additional point is counted without going diagonal, it can be seen that every single eligible end point is an even number, such as two, four, six, eight and so forth all the way up through sixteen.

It has now been established that not every point in a field may be an eligible end point given where the start point is in a field. Taking a start and end point that will yield unicursal paths will produce the next step in understanding the different between 'an original pair' and 'a derivative pair.'

The example below is a 4x4 field that has a start point and an end point added to that field. This combination ('pair') is guaranteed to produce unicursal paths. How many paths that this pair will produce is inconsequential towards the overall goal of defining 'original pairs' and 'derivative pairs.'

Suppose this example was flipped on it's vertical axis (an imaginary line that extends from the top to the bottom, cutting the field in half). This is what the field, still with it's start and end point, would resemble:

And suppose that example was flipped on it's horizonal axis (an imaginary line that extends from the left to right, cutting the field in half). This is what the field, still with it's start and end point, would resemble:

All three pairs are different from one another in terms of where the start and end points are in the field. Yet if all of the possible unicursal paths were drawn from each of these three pairs, a pattern would emerge: The paths would all be the same, merely flipped on either the vertical or horizontal axis.

It would be wasteful to draw paths based upon pairs that produce identical unicursal paths to other pairs. As the fields get larger, the number of paths that each pair may produce grows larger as well. It is helpful in Unicursal Maze Research to only produce the least number of paths that are representative of how many paths there are.

The pairs that are to be used to produce these representative paths will be called 'original pairs.' This designation of 'original' is because this pair is the first to be encountered in this field in this arrangement. Every single additional pair that produces an identical set of paths to this pair will be called a 'derivative pair.' This designation of 'derivative' is because this pair has already been seen before; It is 'derived' from the 'original pair.'

How, though, are original pairs determined? What system may be devised in order to separate original pairs from derivative pairs?

The system that was devised to determine which particular pairs are original and derivative is based upon the initial position of the pair.

The start point begins at the upper-most left corner and the end point begins next to it on it's right. This is the first 'original pair' of every even-numbered field (odd-numbered fields, those fields with an overall odd number of points, are handled slightly differently). All of the derivative pairs for this original pair are then determined. If the field is a square, that square is rotated 90 degrees clockwise three separate times, then the square is flipped vertically from it's original position and that is then rotated 90 degrees clockwise three separate times (for a grand total of eight times: One at the original position and seven to form the derivative pairs).

Each pair, original and derivative, is given it's own unique identification. This identfying name is a three-character alpha-numerical name, from 000 (three zeroes) all of the way to ZZZ. At 36 characters, this system can handle 46,656 total pairs on any given field. This amount of flexibility for the name of a pair is more than adequate for it's application of being a name for an original or derivative pair. Currently, there is no field even hypothetically planned that would stress this limit (for example, an 8x11 field would only use 1,936 names) and any field that would stress this limit would be so huge as to be beyond the scope of current research.

From left to right and from top to bottom, the end point would advance until the start point is forced to move as possible original pairs are eliminated by the acknowledgement of corresponding derivative pairs. This pattern proceeds uninterrupted until all of the possible pairs, both original and derived, are accounted for.

Below are two screenshots of an actual spreadsheet used to determine original and derivative pairs. The field in question is a 4x4 field. The original pairs are designed as black background with white text and derivative pairs are black text on a white background. The 'star' is the starting point and the three-character name is the position of the end point.

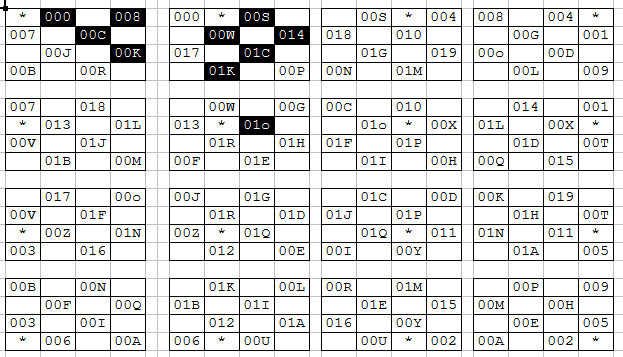
The above information is not an exhaustive learning tool for original pairs, derivative pairs and how to determine them in any given field. However, it should give the uninitiated reader a base understanding of these concepts for when they are discussed later in this website.