The process that occurs to incrementally create a completed path is called a cycle.

In relation to Unicursal Maze Research, a cycle is the complete process of examining an incomplete path (or no path at all) and incrementally expanding upon it until it reaches its next available decision point (or the path is completed, whichever occurs first). A series of cycles will occur that will transform an empty field into a completed path.

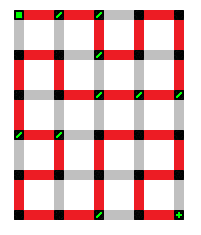
Any completed unicursal path has a start point, an end point and a number of segments equaling one less than the number of points in that field. For example, if the field is 4x4, then there will be exactly fifteen segments attaching all sixteen points (which includes the start and end point). Below is one such example.

Most unicursal paths also contain non-starting decision points (otherwise known as 'decision points') which are points in a field that are not the start point where a path may deviate and still be able to complete the path. These points resemble a forward slash. See the above picture for one such example.

All completed unicursal paths are formed incrementally; They are formed by beginning at the start point and proceeding in a direction until the path is either forced to turn, the path reaches a decision point or the path is completed by reaching the end point.

The direction that a path may take from any interior point is restricted to North, East, South and West (which may also be referred to as 'Up, Right, Down and Left'). Edge points and corner points are further restricted in only those directions where other points in the field are attached. For the purposes of unicursal maze research, these directions are numbered as 1, 2, 3 & 4, respectively. It is not a coincidence that this labelling system is similar to that of an analog clock, with the numbers becoming increasingly larger when rotating through the directions in a clockwise (the minute hand rotating towards your right as you face the clock) manner.

When a new segment is added onto the path in a given direction, the process stops so that the incomplete path may be assessed. The question that the path creator must ask themselves is always: Can I complete this path from the current end of the path in two or more directions? If they can, then the point at which they are currently at is called a decision point and is marked as such with a forward slash. If they can't, then that means that another segment must be added so that another assessment may be made.

Segments are added onto the incomplete path until either a decision point is created or the path reaches the end point. Once a decision point is created, the path creator would then return to the original iteration of the incomplete path and place a segment in the next available direction. For instance, if the first available direction was up (#1) and that direction is now exhausted, the creator would then proceed to the next available direction, which would be to the right (#2). This process would continue until all four directions are addressed. Granted, an incomplete path will rarely have all four directions available for a cycle unless the start point is not in a corner or edge point, at which case all four directions would be available because the path has not been started yet.

Here is an example of a cycle in order to demonstrate these concepts clearly:

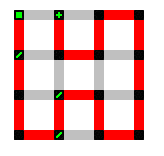
Above is a typical unfinished path, a 5x6 determined path, 0506-01E-232-U. In order to take this unfinished path and perform a complete cycle on it, the following steps need to occur.

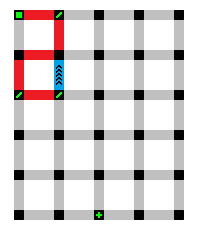
The path can clearly not go up as that would collide with a point that has already been traveled through.

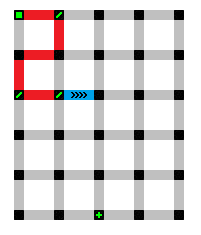
In a clockwise fashion, the next candidate would be to the right. After an expansion of only one segment, it is time to see if there can be a completed path using two or more directions from this point. If so, that would mean that this particular point is a decision point and the expansion would stop here to reflect that development.

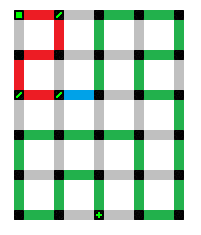
Again, in a clockwise fashion, the first test to see if this new expansion is valid is if a path may be created by going up. It is important to note that not all completed paths going up need to be created; Just one. Here is one such example.

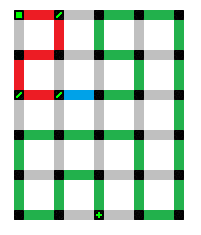
The next direction to attempt in order to see if this is a valid expansion is to the right, continuing with our clockwise order. Again, only one completed path needs to be created in order to demonstrate that this direction is valid. One such path has been created for illustrative purposes.

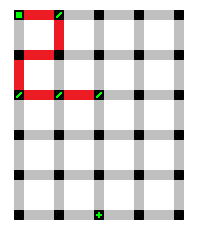
With two directions demonstrating that they can have completed paths, the criteria for that expansion to be valid has been met. A decision point may now be placed at that point. Finding a completed path for the third direction (down) is unnecessary; During this process of the cycle, the only responsibility is demonstrating that the expansion is valid. It is time to focus attention on the final possible expansion for this unfinished path.

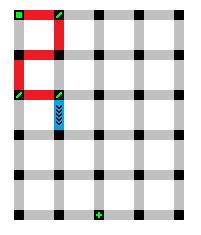
Just as before, an expansion of the unfinished path has been created. Experience clearly would dictate that the only available direction would be to the left but it is always good practice to never assume that a path may be completed unless you trace the path out, either physically or in your mind.

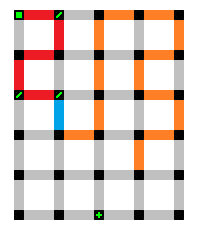
Here is a hypothetical (and futile) attempt for the path to go the right. It obviously is going to be incomplete. However, looks can always be deceiving. When in doubt, always make an attempt to trace out a completed path before dismissing a direction.

The next direction, down, also is not a valid direction, as can be demonstrated in the above picture. That only leaves one possible direction, to the left. If there is only one direction to take at any given point then that point doesn't get a decision symbol on it. The path needs to continue until it does reach a decision point or it reaches the end point.

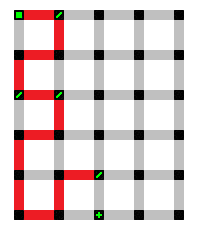
As is demonstrated, going to the left has caused the path to go in different directions before finally reaching a decision point. Regardless for how long and in how many directions this expansion occurred, the path needs to be labeled as having gone down because that was the initial direction. It is now time for the path, regardless if it is completed, to be named. Therefore, this unfinished path shall be called "0506-01E-2323-U."

When a path reaches a new decision point or it is complete, it is named. The naming convention for all paths, complete or otherwise (with one exception), is as follows:

#### is the field dimension. The columns are listed first and then the rows. For instance, if the field that you are working is 5 columns and 6 rows of points, "####" would be "0506." This field is capable of a capacity for fields up to an including 99 columns and 99 rows which is far beyond the capabilities of my current research. Hypothetically, it could be extended to six numbers which would make a 5x6 field be "005006" and so forth.

$$ may either be the numeric or technical name for the original start and end point (the 'original pair'). For instance, if this was the 14th original pair of a 5x6 determined field, the "$$" would either be "14" (the numeric name) or "01E" (the technical name). Either one is acceptable for informal analysis but the technical name should be used for analytical purposes.

%%%%%% is the series of directions that a path has traveled immediately after a decision point (non-starting decision point or, if the path permits it, a starting decision point). An expansion may travel several segments and in several different directions but only the initial direction after the decision point matters.

& represents the letter designation of the path itself. U is used for when a path is unfinished (the path has not yet gone through a cycle). D is used when a path is done (it has gone through a cycle and is now exhausted of options). C is the letter for when a path is complete (the path has been completed from start point to end point as a result of another path going through a cycle).

In rare circumstances, X is used for when a mistake has been made. In fact, these paths are given the designation of X-####-$$-%%%%%%-X (or, amongst older mistakes, XAAAA-BB-CCCCCC-X) so that they are clearly marked and removed from the rest of the cycles. Here is an actual mistake made (X-0505-09-243-X):

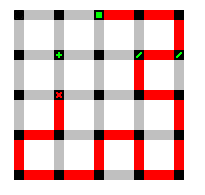
The above information is not an exhaustive learning tool for cycles and how to use them in creating your own unicursal paths. However, it should give the uninitiated reader a base understanding of these concepts for when they are discussed later in this website.